TEMPERATURE SWING ADSORPTION PROCESSES FOR GAS SEPARATION

PDF Publication Title:

TEMPERATURE SWING ADSORPTION PROCESSES FOR GAS SEPARATION ( temperature-swing-adsorption-processes-for-gas-separation )

Previous Page View | Next Page View | Return to Search List

Text from PDF Page: 209

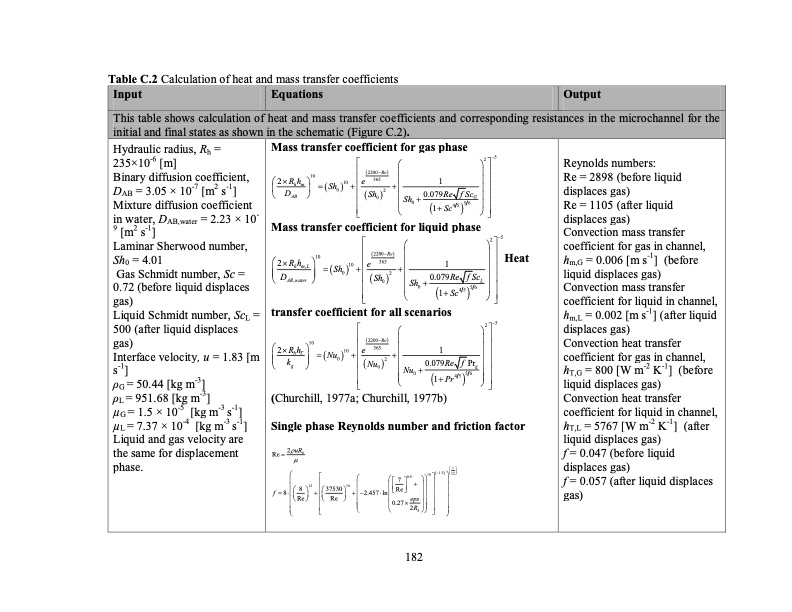
Table C.2 Calculation of heat and mass transfer coefficients Input Equations Output This table shows calculation of heat and mass transfer coefficients and corresponding resistances in the microchannel for the initial and final states as shown in the schematic (Figure C.2). Hydraulic radius, Rh = 235×10-6 [m] Binary diffusion coefficient, DAB = 3.05 × 10-7 [m2 s-1] Mixture diffusion coefficient Mass transfer coefficient for gas phase Reynolds numbers: Re = 2898 (before liquid displaces gas) Re = 1105 (after liquid   2 5  2200Re     365  10 2Rh 10 e  1   hmSh0 2   DAB  Sh0 Sh0.079RefScG  0 4556   1Sc  Mass transfer coefficient for liquid phase 2Rh 10  365  hm,L 10e 1   2 5    2200Re  Heat   Sh  02  DAB,water   Sh0 Sh 0.079Re fScL    transfer coefficient for all scenarios  2200Re   10 365   0 4556   1Sc    2 5    2Rh 10e 1   h T  Nu      k  0 g  Nu2 0.079RefPr  0Nu0 g 56   1Pr45   in water, DAB,water = 2.23 × 10- 9 [m2 s-1] Laminar Sherwood number, Sh0 = 4.01 Gas Schmidt number, Sc = 0.72 (before liquid displaces gas) Liquid Schmidt number, ScL = 500 (after liquid displaces gas) Interface velocity, u = 1.83 [m s-1] ρG = 50.44 [kg m-3] displaces gas) Convection mass transfer coefficient for gas in channel, hm,G = 0.006 [m s-1] (before liquid displaces gas) Convection mass transfer coefficient for liquid in channel, hm,L = 0.002 [m s-1] (after liquid displaces gas) Convection heat transfer coefficient for gas in channel, hT,G = 800 [W m-2 K-1] (before liquid displaces gas) ρL = 951.68 [kg m-3] μG = 1.5 × 10-5 [kg m-3 s-1] μL = 7.37 × 10-4 [kg m-3 s-1] Liquid and gas velocity are the same for displacement phase. (Churchill, 1977a; Churchill, 1977b) Single phase Reynolds number and friction factor Re  2uRh   1    0 . 9   1 6    1 . 5    1 2  12 16 7  f 8 8  37530 2.457lnRe       Re  Re   0.27eps      2R     h  Convection heat transfer coefficient for liquid in channel, hT,L = 5767 [W m-2 K-1] (after liquid displaces gas) f = 0.047 (before liquid displaces gas) f = 0.057 (after liquid displaces gas) 182

PDF Image | TEMPERATURE SWING ADSORPTION PROCESSES FOR GAS SEPARATION

PDF Search Title:

TEMPERATURE SWING ADSORPTION PROCESSES FOR GAS SEPARATION

Original File Name Searched:

PAHINKAR-DISSERTATION-2016.pdf

DIY PDF Search: Google It | Yahoo | Bing

CO2 Organic Rankine Cycle Experimenter Platform The supercritical CO2 phase change system is both a heat pump and organic rankine cycle which can be used for those purposes and as a supercritical extractor for advanced subcritical and supercritical extraction technology. Uses include producing nanoparticles, precious metal CO2 extraction, lithium battery recycling, and other applications... More Info

Heat Pumps CO2 ORC Heat Pump System Platform More Info

CONTACT TEL: 608-238-6001 Email: greg@infinityturbine.com | RSS | AMP